メニューに戻る

15:50 にページが自動更新されます。

摩擦速度と管摩擦係数

学籍番号
氏　　名
図に示すような分岐・合流する四つの管路を通って水（密度 \( 1000 kg/m^3 \)）が水槽 I から II に流れている．
管路①から④の直径，長さはそれぞれ\( d_1 = 250\ mm, L_1 = 700\ m, d_2 = 250\ mm, L_2 = 400\ m, d_3 = 150\ mm, L_3 = 700\ m, d_4 = 300\ mm, L_4 = 1100\ m \)である．
\( H = 15\ m\) の場合の各管を流れる流量を求めなさい．
ただし，管摩擦係数は \( \lambda_1 = 0.0197, \lambda_2 = 0.0205, \lambda_3 = 0.0222, \lambda_4 = 0.0199 \) とし，摩擦以外の損失は無視する．
(A) 流線\(B ② C\)間のエネルギー式の左辺は？ \(\rho Q_2 \times \Large \left[ \right.\) () \(\Large \left. \right] \normalsize W\)
(B) 流線\(B ② C\)間のエネルギー式の右辺は？ \(\rho Q_2 \times \Large \left[ \right.\) () \(\Large \left. \right] \normalsize W\)
(C) 流線\(B ③ C\)間のエネルギー式の左辺は？ \(\rho Q_3 \times \Large \left[ \right.\) () \(\Large \left. \right] \normalsize W\)
(D) 流線\(B ③ C\)間のエネルギー式の右辺は？ \(\rho Q_3 \times \Large \left[ \right.\) () \(\Large \left. \right] \normalsize W\)
(E) (A)=(B)の式と(C)=(D)の式を比較するとどのような関係式が導き出されるか？ \(\) () \(m\)
(F) 流線\(B ② C\)間の失ヘッド\( h_{lB ② C} \)は？ \(h_{lB ② C} =\) () \(m\)
(G) (F)式の関係を連続の式\( Q = A v \)から\( v_2 \)を\( Q_2 \)で表すと？ \(h_{lB ② C} = Q_2^2 \times \) () \(m\)
(H) 流線\(B ③ C\)間の損失ヘッド\( h_{lB ③ C} \)は？ \(h_{lB ③ C} =\) () \(m\)
(I) (H)式の関係を連続の式\( Q = A v \)から\( v_3 \)を\( Q_3 \)で表すと？ \(h_{lB ③ C} = Q_3^2 \times \) () \(m\)
(J) \( h_{lB ② C} = k_2 Q_2^2\)と\( h_{lB ③ C} = k_3 Q_3^2\)と表し，BC間に抵抗係数𝑘，流量𝑄の仮想管路を考える．
仮想管路と並列管路における損失ヘッドの関係は？		 \(k Q^2 =\) () \(m\)
(K) (J)を\( Q \)で表せば \(Q =\) () \(m^3/s\)
(L) 並列管路における流量の関係（連続の式）\( Q = Q_2 + Q_3\)にあてはめると？ \(Q =\) () \(m^3/s\)
(M) (L)の関係から，仮想管路と並列管路における抵抗係数の関係は？ \(\Large \frac{1}{\sqrt{k}} \normalsize= \) () \((m^3/s)/m^{1/2}\)
(N) (J)の関係から，管路 ②の流量\( Q_2 \)は？ \(Q_2 =\) () \(m^3/s\)
(O) \(k_1\)値は？（有効数値３桁で解答） \(m/(m^3/s)^2\)
(P) \(k_2\)値は？（有効数値３桁で解答） \(m/(m^3/s)^2\)
(Q) \(k_3\)値は？（有効数値３桁で解答） \(m/(m^3/s)^2\)
(R) \(k\)値は？（有効数値３桁で解答） \(m/(m^3/s)^2\)
(S) \(k_4\)値は？（有効数値３桁で解答） \(m/(m^3/s)^2\)
(T) \(Q\)値は？（有効数値３桁で解答） \(L/s\)
(U) \(Q_2\)値は？（有効数値３桁で解答） \(L/s\)
分岐・合流する管路の流量

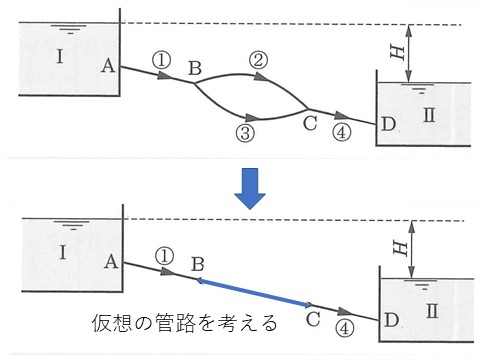
図 分岐・合流する管路の流量



選択肢

(1)\(\lambda_3 \Large \frac{L_3}{d_3} \frac{v_3^2}{2g}\) (2)\(\left( \Large \frac{1}{\sqrt{k_2}} \normalsize + \Large \frac{1}{\sqrt{k_3}} \normalsize \right)\sqrt{k}Q\) (3)\(\lambda_3 \Large \frac{L_3}{d_3} \frac{1}{2g} \normalsize \left( \Large \frac{4}{\pi d_3^2} \normalsize \right)^2\)
(4)\(\Large \frac{1}{\sqrt{k_2}} \normalsize + \Large \frac{1}{\sqrt{k_3}} \normalsize\) (5)\(\sqrt{\Large \frac{k_2}{k}} \normalsize Q_2 = \sqrt{\Large \frac{k_3}{k}} \normalsize Q_3 \) (6)\(k_2 Q_2^2 = k_3 Q_3^2 \)
(7)\(\Large \frac{p_C}{\rho} \normalsize + \Large \frac{v_2^2}{2} \normalsize + g z_C + g h_{lB ③ C}\) (8)\(\lambda_2 \Large \frac{L_2}{d_2} \frac{v_2^2}{2g}\) (9)\(\lambda_2 \Large \frac{L_2}{d_2} \frac{1}{2g} \normalsize \left( \Large \frac{4}{\pi d_2^2} \normalsize \right)^2\)
(10)\(\sqrt{\Large \frac{k}{k_2}} \normalsize Q\) (11)\(h_{lB ② C} = h_{lB ③ C}\) (12)\(\Large \frac{p_B}{\rho} \normalsize + \Large \frac{v_2^2}{2} \normalsize + g z_B\)
(13)\(\Large \frac{p_C}{\rho} \normalsize + \Large \frac{v_2^2}{2} \normalsize + g z_C + g h_{lB ② C}\) (14)\(\sqrt{\Large \frac{k}{k_3}} \normalsize Q\)