| 学籍番号 |
| 氏 名 |
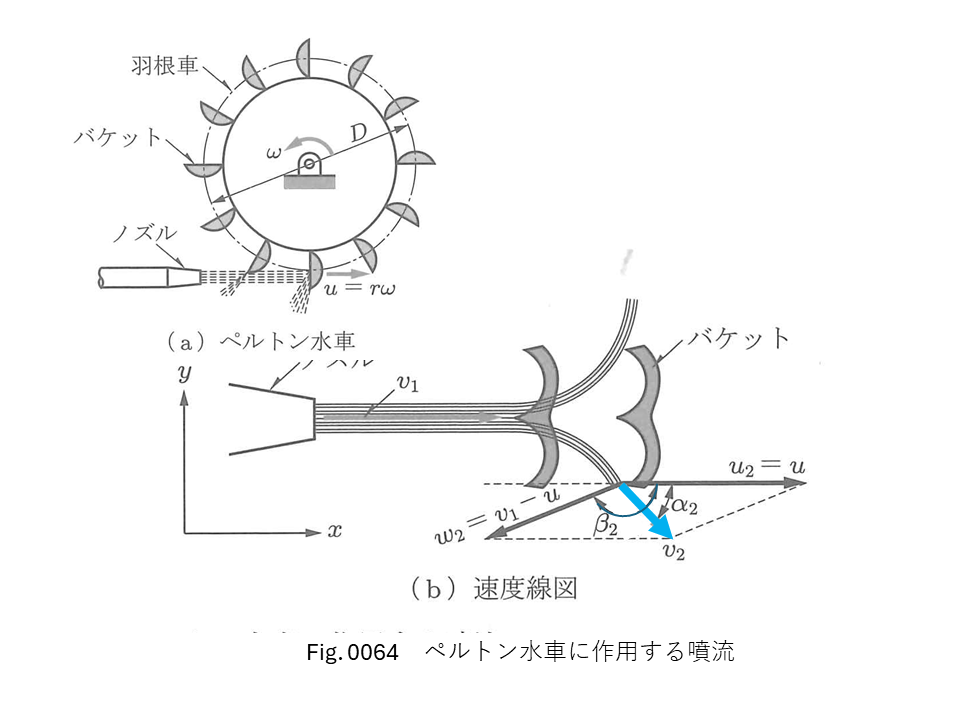
図のように密度\( \rho \)の流量\( Q_j \)の噴流が\( u ( < v_1 ) \)の速度で移動する多数のバケットに与える力の噴流方向の成分\(F_x\)および動力\(P\)をもとめなさい。
なお、絶対座標から見た噴流速度\(v_1\)とすると、噴流の流量 \(Q_j = A v_1\)である。
また、噴流の相対入角は 0°、相対流出角は\(\beta_2 > 90^\circ\)、絶対流入角は 0°、絶対流出角は\(\alpha_2\)である。
文字の入力例:\(\rho \rightarrow\) rho, \(\alpha_2 \rightarrow\) alpha_2, \(\beta_2 \rightarrow\) beta_2, \(u^2 \rightarrow\) u^2,
\(\sin{ \alpha_2} \rightarrow\) sin(alpha_2), \(\cos{ \alpha_2} \rightarrow\) cos(alpha_2) |
| (1) | 移動するバケットに流入する噴流の相対速さ\(w_1\)を\(v_1,u\)で表す。 \(w_1\) = |
| (2) | 移動するバケットから流出する噴流の相対速さ\(w_2\)を\(v_1,u\)で表す。 \(w_2\) = |
| (3) | 噴流はバケットに衝突すると左右に分割されバケットに沿って流れる。
バケットの片側を流れる流量\(Q\)を\(A,v_1,u\)で表す。 \(Q\) = |
| (4) | \(\rho, Q, v_1, u\)で表す単位時間に片側のバケットへ流入する噴流の運動量の大きさ = |
| (5) | \(\rho, Q, v_1, u\)で表す単位時間に片側のバケットから流出する噴流の運動量の大きさ = |
| (6) | \(\rho, Q, v_1, u\)で表す単位時間に片側のバケットへ流入する噴流の運動量の\(x\)成分 = |
| (7) | \(\rho, Q, v_1, u\)で表す単位時間に片側のバケットへ流入する噴流の運動量の\(y\)成分 = |
| (8) | \(\rho, Q, v_1, u, \beta_2\)で表す単位時間に片側のバケットから流出する噴流の運動量の\(x\)成分 = |
| (9) | \(\rho, Q, v_1, u, \beta_2\)で表す単位時間に片側のバケットから流出する噴流の運動量の\(y\)成分 = |
| (10) | 流体が片側のバケットから受ける力\(F_x\)を\(\rho, Q, v_1, u, \beta_2\)で表す。 \(F_x\) = |
| (11) | 流体が片側のバケットから受ける力\(F_y\)を\(\rho, Q, v_1, u, \beta_2\)で表す。 \(F_y\) = |
| (12) | 片側のバケットが流体から受ける力\(D_x\)を\(\rho, Q, v_1, u, \beta_2\)で表す。 \(D_x\) = |
| (13) | 片側のバケットが流体から受ける力\(D_y\)を\(\rho, Q, v_1, u, \beta_2\)で表す。 \(D_y\) = |
| (14) | 片側のバケットが流体から受ける動力\(P_h\)を\(\rho, Q, v_1, u, \beta_2\)で表す。 \(P_h\) = |
| (15) | バケットが流体から受ける動力\(P\)を\(\rho, Q_j, v_1, u, \beta_2\)で表す。 \(P\) = |
| (16) | \(w_2\)と\(u, v_2, \alpha\)の関係は第二余弦定理を用いると、\(w_2^2\) = |