メニューに戻る

１時間後にページが自動更新されます。

角運動量保存則 \( \omega \)(ギリシャ文字) と \(w \)（アルファベット）は文字の形はよくにているので注意
テキスト４．5．３の解説問題

学籍番号
氏　　名
下図は角速度 \( \omega \)で回転する散水器のある瞬間のノズル噴流の様子を示している．
角速度 \( \omega \)、散水器に働くトルク \( T_S \)の関係式を以下の手順にしたがって求めなさ．
なお,水の密度\( \rho \),散水器の各ノズル噴流の流量は \( Q \)である．
反時計まわりのトルク・角運動量は正の値,ベクトルは \( \vec A \)、その大きさは \( A (\,=\, |\vec A|) \) のように表すことにする．
速度大きさ\( r \)方向成分\( \theta \)（円周の接線）方向成分
\( \vec r \)\(r\)\(r \)\(0\)
\( \vec u \)\(u\)\(0 \)\(-u\)
\( \vec v \)\(v\)\(v_r \,=\,v \times \)()\(v_\theta \,=\,v \times \)()
\( \vec w \)\(w\)\(w_r \,=\,w \times \)()\(w_\theta \,=\,w \times \)()

(1) 絶対座標から見た片方のノズル噴流の運動量の大きさは \( \rho Q \times\)()となり,\( \theta \) 方向成分は \( \rho Q \times \)()となる．
(2) 絶対座標から見たノズル噴流の角運動量の大きさは ()\( \times \) \( \rho Q \times\)()となる．
次にノズル断面積を \( A \) とすると, ノズル噴流速度は\( w \,=\, \frac{Q}{A}\) と表せるので,流出する角運動量を \( w \) で表すことを考える．
(3) ノズル位置の周速 \( u \,=\,\)()\( \times \)()
(4) ノズル位置の周速度 \( \vec u \), ノズル噴流の絶対速度 \( \vec v \) , ノズル噴流の相対速度（ノズルから見た速度） \( \vec w \) の関係は \( \vec v \,=\,\)()\( + \)()
(5) (4)の \( \theta \) 方向成分の関係は \( v_\theta \,=\,\)()\( - \)()
(6) (5)を(2)に代入すれば, ()\( \times \)\( \rho Q \times \) [ ()\( - \)() ]が、流出する角運動量となる．
(7) 角運動量保存則は、
() \(-\) 流入する角運動量 \(=\) ()
なので,壁面から流体に作用するトルクを \( T_F \) とすれば流体から壁面（散水器）が受けるトルク \( T_S \) は
作用と反作用の関係から,\( T_F = -T_S\) である．
(8) 散水器では流入が \( r\,=\,0 \) の位置であるから（流入する角運動量）\( \,= \,0 \) である．
散水器はノズルが2つあるので,散水器に働くトルク \( T_S \)
\( T_S \,=\, 2 \times \)()\( \times \)\( \rho Q \times \) [ ()\( - \)() ]
(9) (8) \( T_S \) の値が負の場合は時計まわりの回転トルクとなるので, \( T_S \) の大きさとしては,
\( 2 \times \)()\( \times \)\( \rho Q \times \) [ ()\( - \)() ] > 0


選択肢

(1)\(\Large r\) (2)\(\Large v_\theta\) (3)\(\Large w_\theta\) (4)\(\Large -u\) (5)\(\Large -\vec u\)
(6)\(\Large v\) (7)\(壁面に作用するトルク\) (8)\(流体に作用するトルク\) (9)\(\Large \cos \beta\) (10)\(\Large \sin \gamma\)
(11)\(\Large w_r\) (12)\(\Large -\vec w\) (13)\(\Large \vec w\) (14)\(\Large \vec u\) (15)\(流入する角運動量\)
(16)\(\Large u\) (17)\(\Large \cos \gamma\) (18)\(\Large \omega (オメガ)\) (19)\(流出する角運動量\) (20)\(\Large v_r\)
(21)\(\Large w\) (22)\(\Large \sin \beta\)

7月24日18:30〜　解答公開（2割）


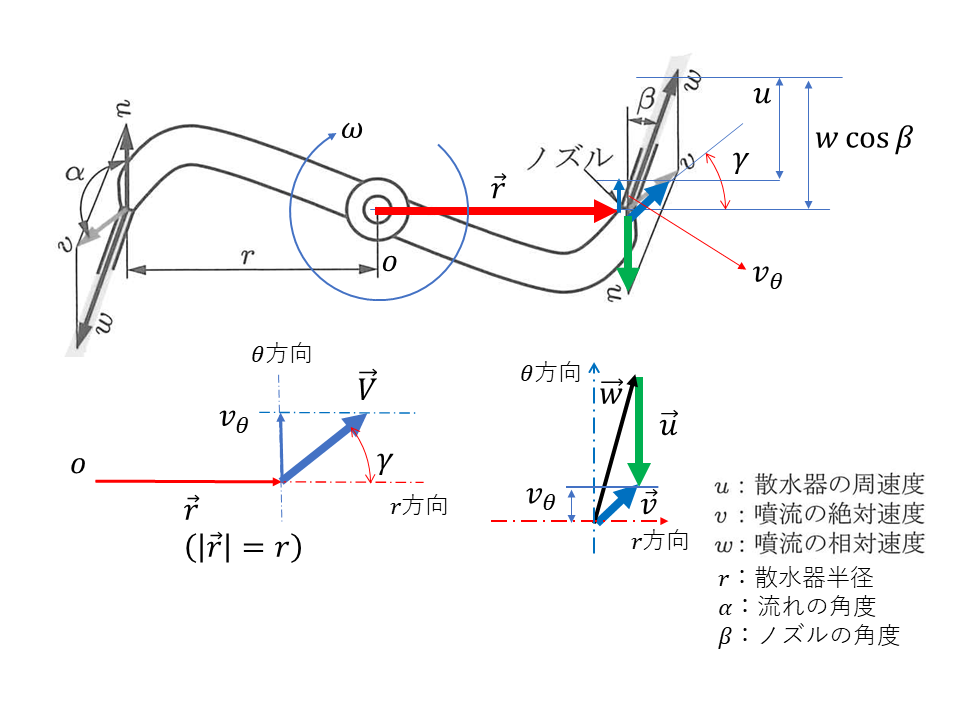
速度大きさ\( r \)方向成分\( \theta \)（円周の接線）方向成分
\( \vec r \)\(r\)\(r \)\(0\)
\( \vec u \)\(u\)\(0 \)\(-u\)
\( \vec v \)\(v\)\(v_r \,=\,v \times \cos \gamma \)\(v_\theta \,=\,v \times \sin \gamma \)
\( \vec w \)\(w\)\(w_r \,=\,w \times \sin \beta \)\(w_\theta \,=\,w \times \cos \beta\)


(1) 絶対座標から見た片方のノズル噴流の運動量の大きさは \( \rho Q \times v\) となり,\( \theta \) 方向成分は \( \rho Q \times v_\theta \) となる．
(2) 絶対座標から見たノズル噴流の角運動量の大きさは \( r \times \rho Q \times v_\theta \) となる．
次にノズル断面積を \( A \) とすると, ノズル噴流速度は\( w \,=\, \frac{Q}{A}\) と表せるので,流出する角運動量を \( w \) で表すことを考える．
(3) ノズル位置の周速 \( u \,=\, r \times \omega \)
(4) ノズル位置の周速度 \( \vec u \), ノズル噴流の絶対速度 \( \vec v \) , ノズル噴流の相対速度（ノズルから見た速度） \( \vec w \) の関係は \( \vec v \,=\, \vec u + \vec w\)
(5) (4)の \( \theta \) 方向成分の関係は \( v_\theta \,=\, w_\theta - u \)
(6) (5)を(2)に代入すれば, \( r \times \)\( \rho Q \times ( w_\theta - u ) \) が、流出する角運動量となる．
(7) 角運動量保存則は、
流出する角運動量 \(-\) 流入する角運動量 \(=\) 流体に作用するトルク
なので,壁面から流体に作用するトルクを \( T_F \) とすれば流体から壁面（散水器）が受けるトルク \( T_S \) は
作用と反作用の関係から,\( T_F = -T_S\) である．
(8) 散水器では流入が \( r\,=\,0 \) の位置であるから（流入する角運動量）\( \,= \,0 \) である．
散水器はノズルが2つあるので,散水器に働くトルク \( T_S \)
\( T_S \,=\, 2 \times r \times \rho Q \times ( u - w_\theta ) \)
(9) (8) \( T_S \) の値が負の場合は時計まわりの回転トルクとなるので, \( T_S \) の大きさとしては,
\( 2 \times r \times \rho Q \times ( w_\theta - u ) > 0 \)