| 学籍番号 |
| 氏 名 |
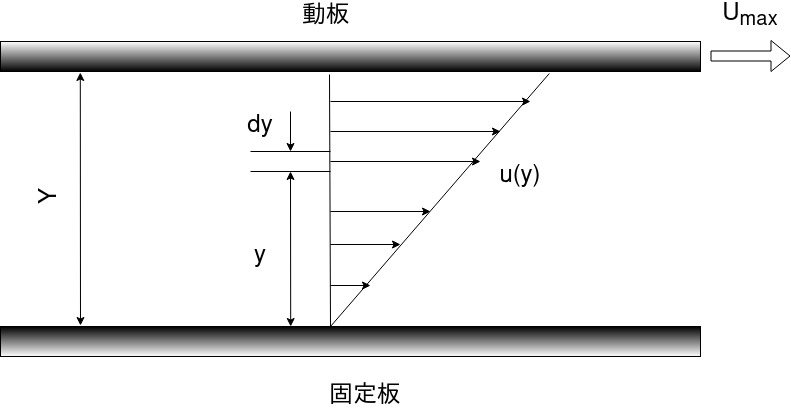
下図のように Y の間隔をもった平行2平板の間に、密度 ρの油が満たされている。
下板を固定して上板を \(U_{max}\)の速度で動かすとき,平板間の速度分布は
\( \Large \frac{ u(y) }{U_{max}} = \frac{y}{Y} \)
で表せる.断面を毎秒通過する運動量の大きさ(\( N \cdot s \))を以下の手順にしたがって求めなさい.なお、奥行きは 1m とする. |
| (1) \( y \)の位置に微小面 \(dS \,=\, 1\) ×() を考えると, |
| (2) 微小面\( dS \)を通過する流量は, \(dQ \,=\, \)() \(dS\) なので、 |
| (3) 微小面\( dS \)を通過する運動量は, \( dM \,=\,\) ()×() \(dQ\) となる. |
| (4) 断面全体を毎秒通過する運動量は,\(M \,=\, \int dM = \, \int_{0}^{Y} \) ()×()×() \( dy \) |
| (5) 流量を \( Q \),断面平均速度を \( U_{ave} \)と表すと \( M \,=\, \)()×\( \rho Q U_{ave}\) となる. |
\( Y = 6 mm \), Umax \(= 1.0 m/s\), \( \rho = 965 kg/m^3\) であれば、
(6) 断面全体を毎秒通過する運動量は () \( N \cdot s\) となる.(有効数値3桁で回答すること.) |